April 27, 2018

A Little Representation of Data: Pixels & Numbers (Lesson the First)

In my standard-issue (non-specialist) Digital Technology classes, I’ve attempted to spruce up the Data Representation content in the course.

I found last year, we neglected poor old Data Rep and focussed a little too much on binary conversions – which led to confusion and distress among some students. ¹

For reasons beyond my understanding or pay grade, Digital Technology is now taken one hour a week for the whole year. There are significant downsides to this timetabling ², but one advantage is that the course content divides somewhat neatly into four terms and having five different classes allows me to refine my lessons and activities to a much finer degree than I could last year (with one class at a time).

For first term, I opted to focus solely on a pixel art activity that I have previously (somewhat optimistically) attempted to squeeze into a single lesson.

The activity essentially guides students through creating an image like this:

Through to a numerical representation like this:

20200000000000000000000000000000000000000000000000000
00000000000000000000001100000000000000000101000000000
00000111001100000000000010000000100000000001000000000
10000000010010000000010000001000000000000100000001111
11001000010000000001011011000100000000001001101001000
00000000000001010000000000000000110100000000000000010
01000000000000000001010000000000000000001000000000000
000000000000000000000000000000000

The fast students will get to the stage of writing clear and simple English instructions to read the numbers and recreate the image (as pixel art), but in my 6-7 lessons, I only managed to get the majority of students performing the numerical conversions.

Lesson 1

(The first set of slides can be found here)

It would be remiss of me not to link to the excellent Digital Technologies Hub section on Data Representation in years 7/8.

The flow in DT hub is to cover representation in year 8 only, beginning with binary representation and moving to the way data is encoded and represented numerically.

In addition, my approach to teaching Data Representation is heavily influenced by the CS Unplugged activities collected as Everything is Numbers.

DT Hub’s resources are structured around the ACARA curriculum points which offer tremendous flexibility ³ so there’s no need to follow their suggested progression slavishly.

In WA, our curriculum body has restricted that flexibility somewhat – it is necessary to cover numerical data representation in year 7 before exploring binary representation in year 8.

Truth be told, the content works in any order and there are benefits to either – knowing that data is numbers prior to learning about binary numbers allows for context when it comes to hardware representation of numbers (switches, magnetic polarity etc) ⁴. Doing it in reverse gives a reason for the conversion of data into numbers.

All of this is to simply say that my efforts this time around began with the concept of “thinking” and the idea that computers think of everything as numbers – an attempt to prime students for the relevance of the exercises ahead.

We look at the idea of “abstract representation” – that symbols be a universally understood stand-in for physical objects or concepts (culminating in language itself, numbers etc), using an activity that I shamelessly stole from a PL with James and Bruce.

While this activity (slides 5-12) is not strictly necessary to teach the curriculum, there is value in making clear the fact that the way computers store abstract representations of our data is actually not such a weird concept, it’s something that we humans do too, and in a far less explicit manner.

The activity from slide 13 onwards is the real introduction to the process of converting a “natural” image ⁵ into pixels and ultimately numbers.

We begin by drawing a simple image of our choosing onto graph paper, ignoring where the grid lines are relative to our drawing⁶. There is an example of a simple picture on slide 15, but I like to draw directly onto the whiteboard with the grid projected to make the process clear.

Students are then to go around squares that encompass the outline of their image and decide, square by square if more than 50% of the square is their picture, or if it is the background. If more than 50% is covered by their picture, they must colour in entire square, if not, the square is left blank.

It is important for students to realise that pixels are an either/or thing (or, in fact, a binary thing) – they may not partially shade a square. If they are unconvinced, have them peer closely at the screens in front of them – there are no half measures with pixels ⁷.

Using the example above, you would end up with something like this:

Natural image converted to “pixels”

Some students are resistant to this stage because:

It destructively edits their artwork
The resulting blocky thing looks a bit rubbish

That’s good – it makes for excellent discussion fodder. Tell them to push through it.

This brings us to the end of my first lesson on data representation.

In the next lesson, students will look at recreating their hand-drawn representation on screen (and the artistes mentioned above will have an opportunity to improve the pixel version) and then figuring out how to convert that to numbers.

Opportunities for Enrichment & Real World Context

The process by which students take their “natural” image and selectively colour in pixels is akin to the process taking place when a picture is taken in a digital camera.

Photography as a medium is effectively “painting with light” – coloured light enters through a lens and strikes a digital sensor ⁸. The digital sensor has the capacity for a certain number of pixels – usually in the tens of millions as at the time of writing this.

The camera has to make the same kinds of decisions as the students – which pixels to turn wholly one colour or the other.

For our students, the process is slightly simplified as we work in true black and white – only one colour – and we are working with a resolution not much more than 20×20 pixels.

My slides include a representation of the same pixels-on-a-grid image but drawn over pixels half the size (therefore, twice as many pixels or twice the resolution). Students can see that increases in the number of pixels per area of image will result in a more faithful representation of the natural image.

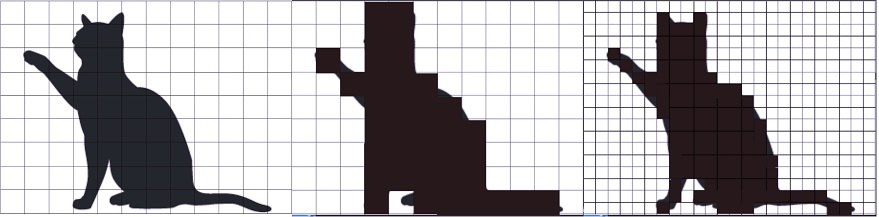
From L-R: A “natural” image, very low resolution, double resolution. Original image is “bleeding” outside the lines to demonstrate the process the students should be following by hand.

Students should also be able to see pretty soon that there are drawbacks to higher resolutions – twice the resolution means twice the number of pixels to “process” and remember, which links very neatly to the reasons why a video game will require more power at a higher resolution or why a better quality photograph will require more space on a hard disk.

April 20, 2018

A Cryptic Education – Substitution and Steganography

As part of the digital technology curriculum, I’ve been tweaking and testing some lessons on cryptography with my year 9 STEM ICT specialist class.

As an opener, we considered a scenario in which one needed to get a secret message to a friend but couldn’t use the now traditional suite of electronic methods available in the average teenager’s tool belt (perhaps their parents are aggressively monitoring their device use?).

The method had to be very low tech – a handwritten note passed through an intermediary.⁹

What if, I suggested, the intermediary ¹⁰ reads the note and then tells your parents or other people?

Students at this point very reasonably suggested that you hand-deliver the note yourself or, you know, just talk to the person, but I either offered believable excuses or hand-waved them off (depending who you ask).

Suggestions to circumvent Eve’s potential treachery included writing the message in another language, the ol’ lemon juice and fire trick, using the ASCII number representation of each letter ¹¹ and… murder.

I’m reasonably sure the last suggestion was tongue-in-cheek, but I’m watching that particular student a little more closely now.

This is the second time I’ve covered crypto with students around this age and I’m always surprised at how rare it is to find a student familiar with substitution ciphers (commonly Caesar). I guess it’s not a popular option for primary – but it does afford me the a chance to get my students constructing their own cipher tools.

We move on from this to more philosophical ground (with one eye on my assassin student) as I pose the question: “Should we have a right to privacy?”

I’m heartened that after a few minutes conversation, students generally reach a consensus that, yes, people should be able to keep their information private if they wish – no secret fascists here.

To make everyone just a little bit uncomfortable I also force the students to confront the following:

If you aren’t doing anything wrong, why should you be able to hide what you do from the government?
Now we all agree that privacy is vitally important, how do you personally keep your own data safe?
Who knows what websites you visit?

I ask these because I feel it’s necessary to confront three important (in very different ways) concepts.

Where do we draw the line on what should be private?

Students generally fall somewhere in the middle of the spectrum from “Our glorious government intelligence agencies should know everything we think and do” through to “You kent trust the gub’mint! We gots to keep our precious datas safe from EVERONE!”

Which is also heartening, I guess. But they’re ultimately left with the uneasy feeling that there isn’t an easy answer to the question of how we (or our authorities) decide it’s okay to spy on a person’s private communication and the mechanism for doing so.

What action are you taking to keep your data/communication private?

None, that’s what.

Or at least, that’s what the average year 9 decides. They’re a little alarmed to realise that they don’t really think about it.

Who knows what websites you visit?

Students confidently assert that they just use incognito mode or delete their history if they wish to keep their browsing secret.

I point out that their ISP knows everything they do (with timestamps!) unless they first use a tunnel or VPN.

Also, any time they use a gated Internet connection – like the school – the IT staff can summon their browsing history at will.

Some students reconsider their life choices.

Back on track – Steganography

Now that my class has indulged my diversion, we get back on track. I mention that hiding messages – ala the lemon juice, and even arguably using another language – is considered steganography. In steganography, your message is only really secret if the method by which you hid it is kept secret too – if someone knows to look for something hidden, they’ll probably find it. One bright spark suggests writing an innocuous message and then putting the secret, inflammatory message in lemon on top, which is admittedly pretty clever. ¹²

(I don’t use the word obfuscate even though I want to because we just don’t have time to add it to our vocab list – but I think I regret that now. I’m a little tickled by the idea of my ex students wandering around, whipping out five dollar words they learned in ICT.)

We consider the idea of mirror writing – as that’s often trotted out as an example of keeping writing secret in the context of Leonardo da Vinci.

I’m pleased to note that a few students conclude that Leo probably didn’t use mirror writing to keep his work hidden, based on the fact that it’s not that hard to read backwards writing. A few hardened hold-outs insist that it would stop the average interloper casually reading over his shoulder, which is a fair assessment, but even they grudgingly give way when I point out that most people in his time were illiterate anyway, and he was (crucially) left-handed. We decide for now that his mirror writing was probably more for convenience than an effort to maintain secrecy. ¹³

As a final nail in the coffin of the effectiveness of mirror writing as a tool of secrecy, I display the following slide, with the commentary that it is actually pretty challenging to read mirror text fluently:

This exercise is pretty mundane in and of itself, but in a class of competitive over-achievers, it is a thing of beauty.

All the students spontaneously and simultaneously break forth in a halting reading chant, reminiscent of early years primary students:

“I…. DON’T…. LIKE…. YOUR…. LITTLE…. GAMES….”

I secretly wish for someone important to barge into the room at this point and do a double take at our high-flying yet somehow remedial level reading students.

The competitive chant falls apart around 2/3 of the way through as a sufficiently large number of students realise I’ve tricked them into reading Taylor Swift lyrics under (somewhat) false pretences.

And with this, we’re pretty much out of time.

There’s an opportunity to recap concepts (privacy, hiding messages) before we’re done.

And after a whole lesson on cryptography, we haven’t actually covered any cryptography.

Boring ed stuff: LI ¹⁴ SC ¹⁵
Looking for a link to the slides? You can find it here.

April 5, 2017

Official RPi Touch Display – GPIO damaged by improper wiring

Some of my students have access to hardware for their projects and experiments, including various Raspberry Pi-s and alternative ¹⁶ operating systems and accessories.

Unfortunately, given the way the Pi interacts with HATs ¹⁷ and other similar devices via GPIO ¹⁸ pins, there is always the possibility that 5V will go where it shouldn’t and damage will be done.

In the case of the official Raspberry Pi Touchscreen Display, the device can be wired up to either receive or provide power to the Pi via jumper cables through the GPIO pins or provide power to the Pi via an included USB A port in the more “traditional” way.

When it comes to hobbyist hardware (and software!) there is an impetus to err on the side of giving the user as many options as possible.

When it comes to custom wiring, I think Murphy’s Law ¹⁹ should take precedence over hobbyist convenience. In other words, don’t even give us the option to power it via a method that will release magic smoke if done wrong.

There is some value in allowing users to power the Pi using the pins – and indeed this appears to be encouraged, as the enclosure that ships with the display only provides access to the Pi usb port.

At any rate, multiple options are available and inevitably, one of my students has configured one of the options that puts power where power should not go. As a result, neither the Pi nor the display are giving me any joy now when wired correctly.

It would seem that the Pi is beyond redemption – there is no display via HDMI and the SD card reader is unable to read cards.

The display is a happier story – there is no possibility to push power to or from it via the pins, but it seems perfectly happy to power on and pass power through via the USB port.

So just a quick note to anyone in a similar position – try your “dead” display with another (known working) Pi using the USB ports to provide power to both and you might find the display still has life yet.

April 3, 2017

Domain Specific Vocabulary and the Up Goer Five

If you’re not familiar with the “Up Goer Five”, it’s Randall Munroe‘s schematic of the Saturn V rocket annotated using only the ten hundred ²⁰ most commonly used English words.

(I will not embed it in this post, because it’s HUGE, but feel free to click this here link to see it)

The Up Goer Five spawned Munroe’s book, Thing Explainer, which is an excellent resource for puzzling ²¹ the hell out of students who’ve been studying the topics covered.

Flipping through Thing Explainer got me thinking about how being forced to explain things in absurdly simple terms both often resulted in a more direct and exact description of a component and also (I imagine) challenged the author to avoid the use of domain specific language ²² and consider what, exactly, that vocabulary really means.

Ever since the existence of this text editor, I’ve been keen to throw my students up against the Thing Explainer to force them to really think about what special vocabulary and concepts actually mean – unavoidable if your explanation is to have any real value.

Is there any educational value to this exercise?

I don’t know for sure. But I can think of a few ways in which this might be beneficial:

Domain specific knowledge is tested
A deeper understanding of the concept
Develops the use of literacy skills

Let’s look at how I think the above benefits can be attained.

Tests Domain Specific Knowledge

Students (and teachers!) can become very good at using the right technical language to describe concepts they either don’t understand well or flat out don’t “get” at all. This particularly applies to students who are good at rote learning definitions of things.

Often this regurgitation technique is good enough to get some or all marks for an exam question, but if you don’t understand foundational concepts, you can’t build on those for more advanced concepts.

Removing the use of domain specific language takes away the ability to fudge your answers – in order to explain advanced concepts, the student needs to also explain all the concepts that make it up ²³.

Develops a Deeper Understanding

“Rewording” existing texts is a skill, and it’s one that students generally seem to hate practicing. Rewording using a limited vocabulary actually scaffolds this task – instead of pulling out a thesaurus and substituting vocabulary, students are forced to consider re-explaining the concepts in new ways.

Explaining things in genuinely new ways is (as any teacher would know), one of the best ways to deepen one’s understanding of a topic.

Develops Literacy

Wouldn’t simple language be a poor way to develop literacy?

I would suggest that, no, in fact it should improve students’ literacy by forcing the remapping of more complex and domain specific terms into the simpler language that defines that vocabulary.

Examples and Problems

My example for students was as follows:

A box with a round part inside. Bits of the round part can be turned on or off to remember things. When the power goes off, the round part still remembers. An arm can look at the round part and see the bits that are on and off.
Finding or changing the on and off bits on the round part takes a long time.

We’ve been looking at computer hardware for part of this first term and so they were familiar enough with hard drives to be able to correctly identify the component for that description.

I’ll admit I cheated a little here – the use of the word “bit” can be read both as a colloquialism and in its domain specific form ²⁴. In my original explanation, I reversed the use of “part” and “bit” to deliberately avoid this, but ended up switching them back to avoid confusion.

Instead of the usual technical language describing spinning platters and reading heads and so on, we get to the nub of the issue: a hard drive is for long term storage (remembering) and it’s relatively slow. To differentiate it from other forms of secondary storage we look at some implementation terms (platters are round and an arm with a head is used to read them).

Certainly there are limitations here – it might be nice to be able to use concepts like “magnetism” to really hammer home the physical representation of binary data – but it forces a student who has learned the rote definition of hard drive (“secondary storage that uses magnetic fields to blah blah blah”) to actually consider what a hard drive really is.

Let’s have a look at some student examples:

1.A group of memory that mirrors it self on to another group of memory to keep a back up of what is stored on it.

2. A group of memory that puts half of what is known onto another group memory

We’re describing the concept of RAID – certainly level 1 first up and possibly level 0 second, although in this case I would send it back for further clarification.

1.the pretending of another computer that is run on another thing. It can be used to use the computer from another place.

2.the storing of stuff in many different places so that stuff can’t be lost, and it is easy to get.

3.the same way that a computer is made to be used in work, this means a place for work can have an even and matching thing for use for people.

The first item in this list is a beautiful example of what can be produced using Thing Explainer vocabulary – we’ve avoided all use of the term “simulation” or “virtualisation” to explain what virtual machines are.

As we get towards the bottom of the list, we run into the frustrations or limitations that some students encounter when trying this for the first time – the temptation to overuse words such as “stuff” (when explaining data in cloud storage) or to become fixated on a particular aspect of a concept (when explaining a standard operating environment) can cause an explanation to miss its mark.

When lots of stuff is put into a place so that if the stuff goes away then the stuff can be gotten again.

Despite the overuse of “stuff” in this one, all it really needs is a little context to help clarify that we’re referring to a backup of data.

Worth Pursuing?

All in all, I’m pleased with the results thus far. Students were satisfied with my justification of the activity and quickly saw the value in using this as a revision technique.

Would this work for younger students? I’m not sure, but the opportunity should present itself in the near future.

December 1, 2016

CS Unplugged – Parity with Cards

Age groups used: Year 10s (~15 years)

I’ve been using the most excellent CS Unplugged activities for some of my classes this year – they are predominantly targeted to primary school classes, but they adapt very well to my high school students (either we roll through the activities faster or at a higher level).

It is now nearly two decades since the CS Unplugged activities were published and I think it’s important to note that they are still generally extremely relevant and useful to modern curriculum. Technology is used, implemented and reimagined all the time – but the underlying principles (generally) remain the same.

As a relatively fresh high school teacher, learning how best to position, prime and implement these activities has been a challenge this year – I’d like to reflect and report on how some of these have played out. Continue Reading…

January 9, 2016

Teachers as Practitioners

Should high school teachers be practitioners of the subjects they teach?

It can be a compelling argument – certainly, some graduate art teachers have described to me a requirement to exhibit their work regularly to maintain their qualification and at first blush that seems reasonable (to a non-art teacher).

After all, how can you expect a specialist art teacher to provide the best education in art if they aren’t “an artist” (questions about what constitutes a “professional artist” aside)?

Art’s value has plummeted with one standard US folio fetching only 15.64 USD

Jonathan Ihlein

Developer. Enthusiast. Omnivore.

Category Archives: Teaching